Обертоны и гармоники

Зачем оно вам?

Как вы яхту назовёте.... Видимо, поэтому нашему коллеге с никнеймом @Brainy всё время мало. Наверное, хочет знать вообще обо всём, умник хренов! Ну, а я чо? Мне разве жалко? Сегодня поговорим про обертоны и гармоники, тем более, что в ближайшее время планирую выкатить пост про обертоновую флейту.

Обертон — это любой призвук, звучащий вместе с основным звуком и имеющий бо́льшее число колебаний. Отсюда и название: обер (нем. над) + тон (звук определённой частоты). В английском, кстати, их называют овертонами. И у нас я уже тоже слышал, что так называют. На мой скромный взгляд, это является моветоном. Хватит и того, что наше родное глиссандо слайдом обзывают на аглицкий манер.

Гармоника — частный случай обертона, но напрямую зависящий от основного тона. Если колебание обертона строго кратно колебанию основного тона, например выше него в: 2, 3, 4 и так далее, — раза, то это гармоника.

Для обертона такая зависимость необязательна. Например, плохо прижатая струна будет дребезжать. Дребезг является обертоном, но не является гармоникой.

Откуда же обертоны берутся? Рассмотрим на примере всё той же струны. Если представить поступательное движение звучащей струны на графике зависимости расстояния от времени, то упрощённо мы получим синусоиду, где пики — это движение струны вперёд (вверх), провалы — движение назад (вниз), а переход через ноль — возвращение в исходное положение.

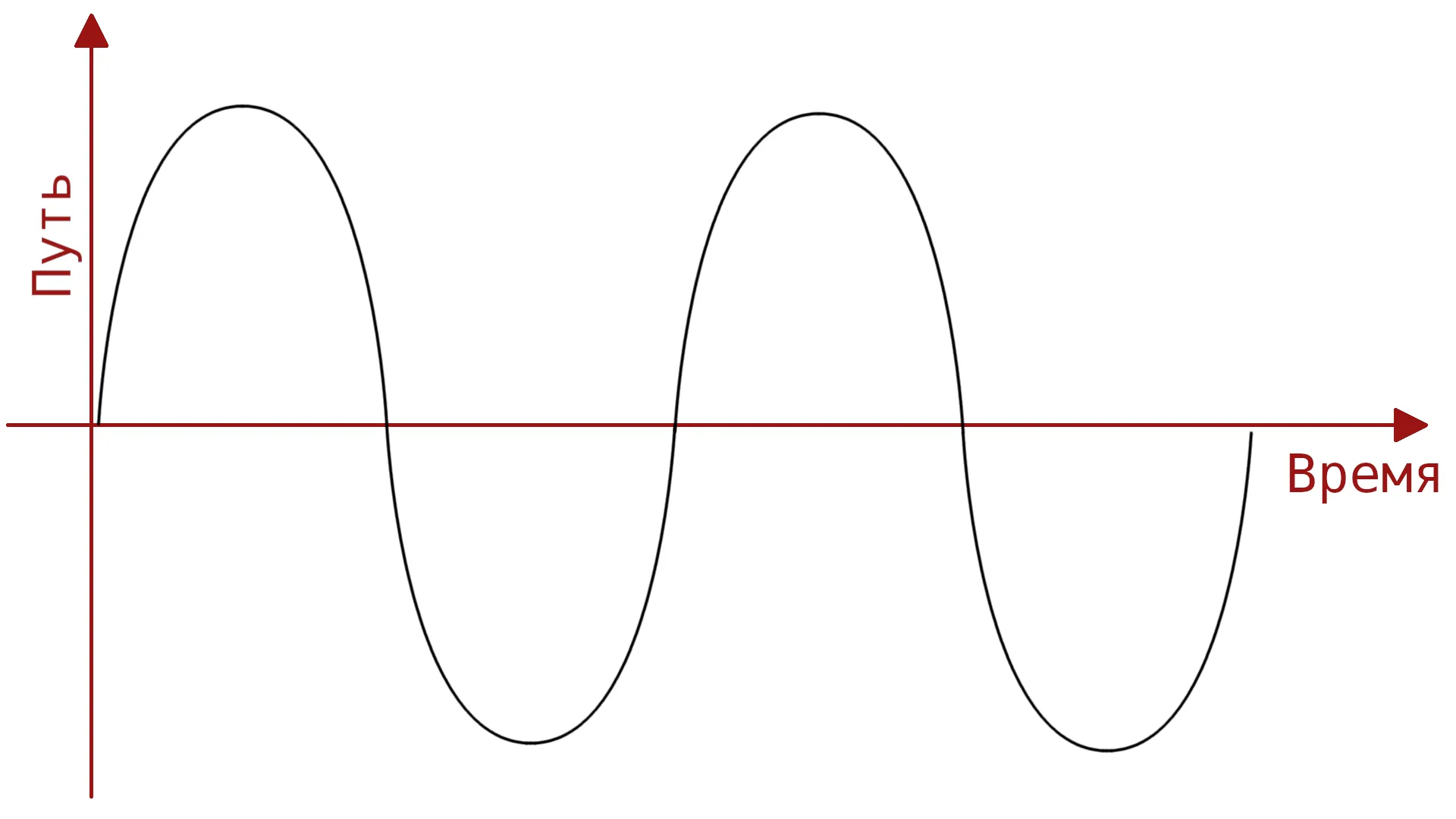
Но в жизни мы такую синусоиду можем увидеть услышать только в генераторе частоты.

Кстати, такие генераторы сейчас уже настолько общедоступны, что скачиваются на любой телефон. Можете поискать в магазине приложений и поиграться с частотами. Заодно убедитесь, что "голая синусоида" звучит весьма грустно и даже близко не напоминает звук гитары, флейты или саксофона. Это потому, что именно обертоны делают звук инструмента уникальным.

Однако, вернёмся к нашей синусоиде. Чистые синусы в природе, как я уже писал выше, практически не встречаются, любое колебание имеет внутри себя ещё колебания. На графике это будет выглядеть примерно так:

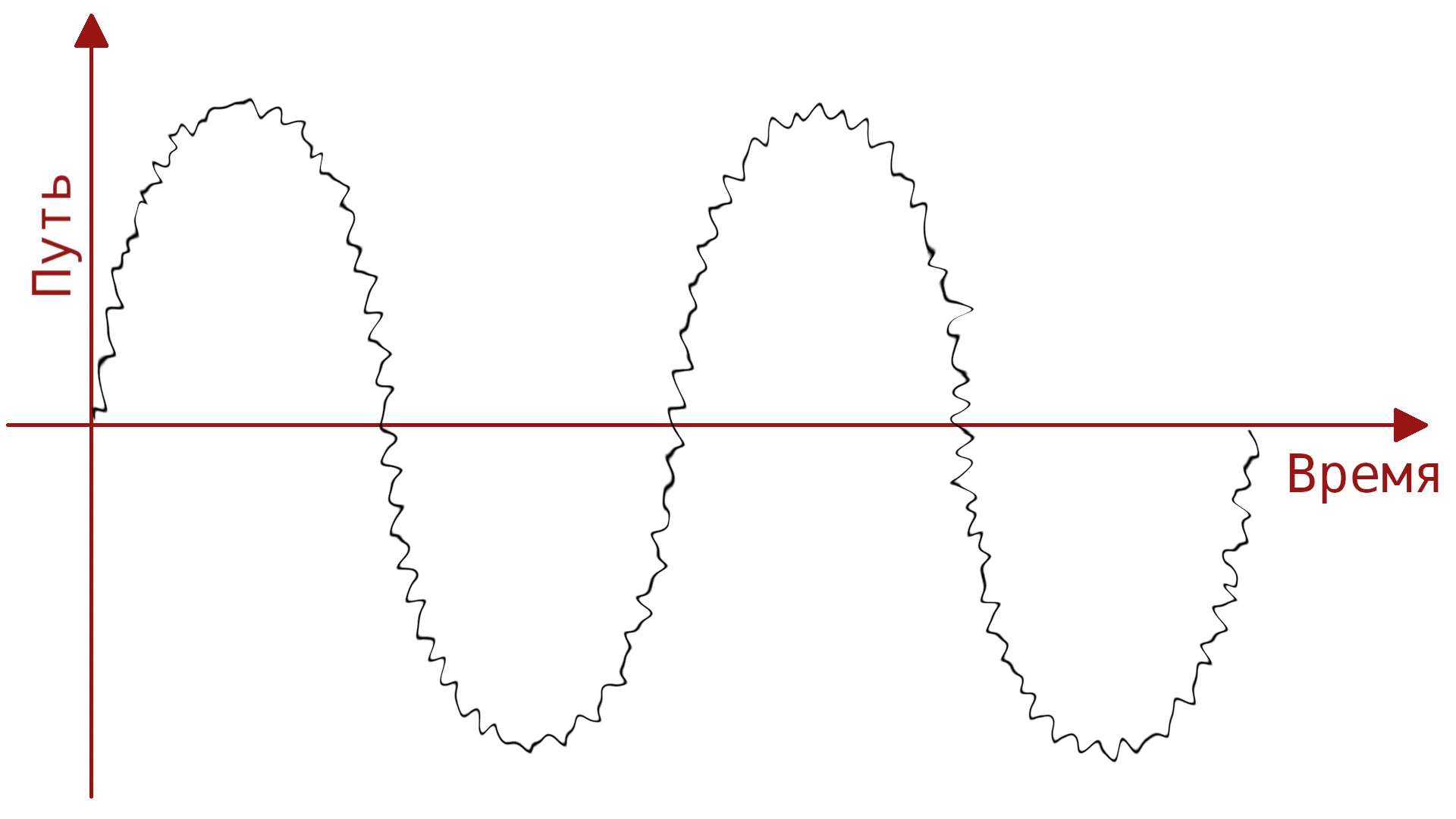
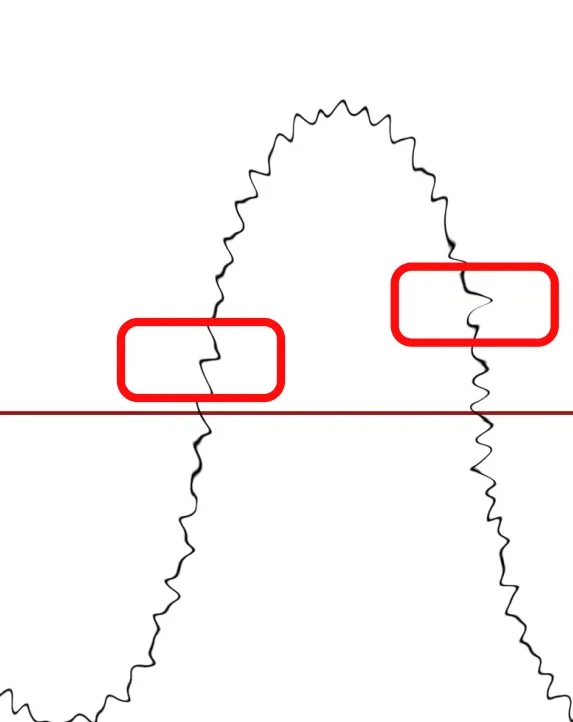
А, если увеличить масштаб, то можно будет разглядеть внутри этих колебаний ещё одни колебания, а внутри них ещё одни и так далее. Это называется порядком: обертоны (или гармоники) первого порядка, второго и т.д.

Пожалуй, на сегодня хватит. Продолжим в следующий раз, если ещё хоть кто-то (кроме умника) припрётся на занятие.